ПРИНЦИП РАБОТЫ ЗАВОДОВ "BUSHHOFF"
Мобильный завод по производству комбикорма - это определенный набор агрегатов, с помощью которых осуществляется размол сырья, добавка в комбикорм премиксов и компонентов в соответствии с Вашей рецептурой , смешивание всех ингредиентов и выгрузка готового корма из накопительного бункера.Мобильные комбикормовые заводы работают по принципу измельчения свободным ударом молотками, шарнирно закрепленными на роторе, вращающемся в дробильной камере со скоростью 35...120 м/с. Материал при встрече с молотками дробится на лету, отбрасывается к стенкам камеры или решету и там за счет полученной кинетической энергии измельчается дополнительно.
Крупность частиц зерновых концентрированных кормов должна быть не более: для КРС — 3 мм, свиней и птицы — 1 мм, если эти концкорма используются для приготовления влажных мешанок. Если используют плющенное или экструдированное зерно, частицы допускаются более крупными. При этом пылевидных частиц должно быть минимально.
Любой корм до и после обработки не должен содержать в себе твердых примесей и металлических включений, семян сорных растений.
Влажность измельченных концентрированных кормов, подлежащих длительному хранению, не должна превышать 14...15 %.
Основы теории измельчения
Как указывалось, измельчение предусматривает разделение твердого тела на части. При этом образуются новые поверхности. Пусть имеется кубическая частица с размером ребра L. Ее общая поверхность составляет: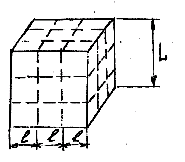
S = 6*L6
Если эту частицу измельчить таким образом, что получится n одинаковых кубиков, тогда длина ребра каждого из них составит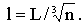
Площадь поверхности каждого кубика будет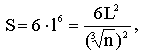
а всех n кубиков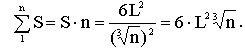
Сравнивая площадь кубика до дробления с суммарной площадью кубиков после дробления, можно написать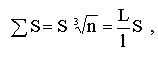
т.е. на сколько частей будет разделено ребро кубика, во столько же раз возрастет суммарная поверхность частиц.
Оценку развитости поверхности сыпучих материалов производят величиной удельной поверхности — отношением суммарной поверхности всех частиц к их массе или объему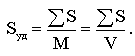
Например, для куба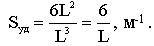
Крупность частиц того или иного кормового материала обуславливается зоотехническими требованиями. Для оценки затрат энергии, требуемой для перевода частиц от исходной крупности к заданной, необходимо знать степень измельчения, которая представляет собой отношение среднего размера частиц до измельчения (L или D) к среднему размеру частиц после измельчения (l или d)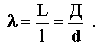
Степень измельчения можно выразить через удельную поверхность частиц. Учитывая, что L=6/Sуд и l=6/Sуд , можно написать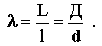
Процесс измельчения часто характеризуется также приращением удельной поверхности частиц: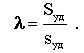
Обычно процесс измельчения изучается с двух позиций:
1. Выявляется зависимость между затратами энергии и степенью измельчения. Это позволяет выявить эффективность рабочего процесса, определить оптимальные рабочие органы применяемых типов машин и режимы их работы.
2. Определяется закономерность распределения измельченных частиц по крупности, что позволяет найти наиболее эффективные способы расчета средних размеров частиц, величин их удельной поверхности и численных значений степени измельчения.
Оба этих вопроса рассматриваются в энергетической теории измельчения.
Чтобы разрушить тело на части, необходимо приложить к нему усилие, большее, чем силы молекулярного сцепления. Силы молекулярного сцепления зависят от физико-механических свойств материала и поэтому могут быть различными. Работа внешних сил, затраченная на измельчение материала и отнесенная к единице массы или объема, называется удельной работой измельчения.
Еще в прошлом веке были предложены две энергетические теории измельчения: поверхностная и объемная. В соответствии с поверхностной теорией измельчения, которую предложил немецкий ученый П. Риттингер (1867 г.), работа измельчения прямо пропорциональна вновь образованной поверхности: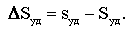
где a — коэффициент пропорциональности, учитывающий величину энергии молекулярного сцепления твердого тела.
Экспериментальные исследования показали, что поверхностная теория измельчения применима лишь при тонком измельчении. Для грубого измельчения русский ученый В.Л. Кирпичев (1874 г.) и немецкий ученый Ф. Кик (1885 г.) предложили объемную теорию измельчения, согласно которой работа измельчения прямо пропорциональна объему деформированной части тела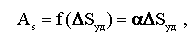
где k — коэффициент пропорциональности;
V — объем деформированной части тела.
Поскольку при измельчении могут получаться крупные и мелкие частицы, П.А. Ребиндер в 1928 г. предложил объединить обе теории в одну и рассматривать общую работу как сумму работ на образование новых поверхностей и деформацию, части объема тела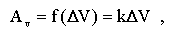
Анализируя приведенные зависимости, нетрудно убедиться, что для практического использования они малопригодны. С одной стороны, тяжело определить численные значения приращения поверхности и объема деформированной части тела, с другой — неизвестны коэффициенты a и k.
В 1952 г. С.В. Мельников предложил приближенную формулу для количественных расчетов работы измельчения в зависимости от степени измельчения: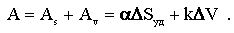
где С1 и С2 — коэффициенты, учитывающие удельные затраты энергии на измельчение и имеющие размерность удельной работы (Дж/ кг), определяются опытным путем. Например, для ячменя С1 = (10...13) 103 Дж/ кг, С2 = (6...9) 103 Дж/ кг.
Как мы уже говорили, при измельчении получаются частицы различного размера и тем более формы. Чтобы каким-то образом упорядочить размер и форму частиц для возможности дальнейших расчетов, принято приводить частицы неправильной формы к шару. При этом его диаметр определяется из фактического объема частицы неправильной формы. Определение объема частицы производят путем погружения отсчитанного их количества в мензурку с жидкостью, имеющий малый коэффициент поверхностного натяжения (керосин, ксилол, толуол и т.п.). Объем частицы определяется делением полученного общего объема на количество частиц в пробе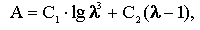
Тогда эквивалентный по объему диаметр частицы: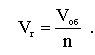
Было бы неправильным для определения эквивалентного диаметра брать частицы резко отличающихся размеров. А какие именно нужно брать?
В любом случае в массе измельченного материала размеры частиц подчиняются закону нормального распределения (закон Пуассона).
Этот график показывает, какой процент (или относительное количество) частиц имеет тот или иной размер. В любом случае частиц малого и большого размеров (диаметра) бывает меньше, чем среднего.
В зависимости от измельчающего рабочего органа кривая Пуассона может быть с высоким пиком или приплюснутая. Как оценить, каких частиц в массе материала больше? Для этого существуют различные методы определения среднего размера частиц: арифметический, геометрический, логарифмический, интегральный, взвешенный. Каждый из методов применим в определенных конкретных ситуациях.
Для практических условий наиболее пригоден метод определения средневзвешенного размера частиц. Это упрощенный среднеинтегральный метод. Если взять площадь под кривой и разделить на 100 % или Р, получим среднеинтегральный размер частиц. Но получить такую кривую сложно, да и обрабатывать ее трудоемко. Проще определить, сколько частиц данного размера находится в общей массе. Тогда получится гистограмма.
По сути она описывается кривой нормального распределения, но получить ее и обработать значительно проще.
Берут навеску разноразмерного материала и просеивают ее на ситах с разным размером ячеек. Размер частиц от 0 до d1 — проход через последнее сито, размер от d1 до d2 — остаток на последнем сите и т.д.
Размеры частиц остатка на первом сите обычно принимают равными:
где m — модуль сита — число, показывающее, насколько размер ячеек одного сита отличается от другого.
Как видно из гистограммы, средневзвешенный размер частиц можно определить по формуле:
Для зерновых кормов средневзвешенный размер частиц называется модулем помола.
В лабораторных анализах используют ситовой классификатор с набором из 10...12 сит с модулем m = 1,41 В производственных условиях используют классификатор из трех сит с размером ячеек 1, 2 и 3 мм. Тогда модуль помола:
где Р0, Р1, Р2, Р3 — процентное содержание фракций.
Для комбикормов принято считать М = 0,2...1 мм — мелкий помол, М = 1...1,8 — средний, М = 1,8...2,6 — крупный помол.
Рабочие органы, рабочий процесс молотковой дробилки
В мобильных заводах «BUSHOFF» применена дробилка закрытого типа с горизонтальным валом, решето и деки охватывают барабан до 300°. Материал удаляется по мере измельчения до заданного размера через отверстия решета.
Комбикормовые заводы «BUSHOFF» оборудованы циклонами с системой трубопроводов и фильтрами-пылеуловителями, образующими единую замкнутую пневмосистему. Это способствует обеспыливанию помещений.К рабочим органам относят молотки, решета и деки.
Для измельчения зерна используют пластинчатые молотки толщиной 6 мм.
Изготавливают молотки из марганцовистой стали 65Г с закалкой рабочих (активных) поверхностей или углеродистой стали с наплавкой кромок сармайтом.
Решета предназначены для отвода готового продукта, дополнительного его измельчения и регулирования степени измельчения. В мобильных заводах «BUSHOFF» применяют гладкие решета из листовой стали с пробивными круглыми отверстиями диаметром от 3 до 10 мм. Живое сечение решет составляет 0,08...0,35.
Процесс измельчения в молотковой дробилке происходит следующим образом. Зерна материала, попав в зону действия молотков, получают первый удар и отбрасываются к периферии, где отражаются поверхностью от деки или решета.
Отражаясь от них, частицы замедляют свое движение, но в зоне действия молотков они опять ускоряются от их ударов и потока воздуха. При установившемся процессе по всей внутренней окружности корпуса дробилки образуется вращающийся непрерывно перемешивающийся слой материала. От многократных столкновений с молотками, решетом и декой зерна измельчаются. При достижении заданного размера частицы материала проходят через отверстия решета и удаляются из дробилки. На их место поступают новые порции неизмельченного материала.
Работа деформации при ударе
Применительно к сельскохозяйственным материалам теорию о работе деформации при одиночном ударе в молотковой дробилке разработал В.П. Горячкин (см. собрание сочинений т.3. -М.: Колос, 1965).
Допустим, что между молотком и частицей происходит не упругий прямой центральный удар. Сопротивление молотку оказывает инерция частицы. В результате удара возникает импульс силы, который равен изменению количества движения:
i = M (vM - vk ), (1)
где М — масса молотка, кг;
vм и vк — скорость молотка до и после удара, м/с.
Если допустить, что начальная скорость частицы vr = 0, то изменение количества движения ее составит:
i = m * vk , (2)
где m — масса частицы, кг;
vк — скорость частицы после удара, равная скорости молотка после удара, м/с.
Импульсы сил, приложенных к частице и молотку, равны, поэтому равны и правые части уравнений (1) и (2)
M (vM - vk ) = m * vk
откуда
M * vM - M * vk = m * vk ,
M * vM = vk * (M + m) ,
или
(4)
Из формулы (4) видно, что конечная скорость зависит от соотношения масс соударяемых тел и изменяется по гиперболе. Если m <= M, то vм = vк.
Определим полезную работу молотка при его ударе по частице. Из курса теоретической механики известно, что при не упругом ударе часть кинетической энергии сохраняется для движения системы соударяющихся тел, а вторая часть превращается в работу деформации этих тел. Если сопоставить прочность молотка и измельчаемого материала, то можно заключить, что деформации и измельчению будет подвергаться менее прочный материал, каковым является корм. Поэтому всю работу деформации с известным допущением можно считать полезной. Найдем ее значение.
Полный запас кинетической энергии молотка при ударе
После удара кинетическая энергия молотка
Если допустить, что начальная скорость частицы ?r = 0, то и ее кинетическая энергия до удара равна нулю. После удара частица приобретает конечную скорость молотка и ее кинетическая энергия:
На основании закона сохранения энергии можно записать
A0 = Aм + Ar + Aдеф
откуда
Aдеф = A0 - (Aм + Ar )
или
Подставим из (3) значение mvk, тогда
(5)
Из уравнения (5) видно, что работа деформации прямо пропорционально зависит от скорости молотка или частицы после удара. При измельчении зерна обычно m < M и конечная скорость vм = vк . Тогда выражение (5) можно записать
(6)
Если m >> M, то конечная скорость ударяющего тела становится равной нулю. Такое явление наблюдается при ударе летящего зерна о деку. Таким образом, полученная от молотка кинетическая энергия зерна также расходуется на его деформацию при ударе о деку.
Тогда полезная работа от удара молотка по зерну составит
(7)
Уравнения для определения работы деформации получены с определенными допущениями.
Чем меньше масса измельчаемой частицы по отношению к массе молотка, тем с меньшим эффектом работает молотковая дробилка.
Необходимо отметить, что работа деформации, вычисленная по формуле (6), является максимально возможной для случая неупругого удара. На самом деле зерно и другие виды кормов обладают определенной упругостью, которая может быть учтена коэффициентом восстановления.
Тогда формулу (7) можно записать
(8)
По опытным данным для зерна средней сухости Купр = 0,3...0,4. Следовательно, при свободном ударе с учетом упругих свойств зерна лишь 84...91 % кинетической энергии от максимально возможной расходуется на разрушение. При измельчении зерна внутри дробильной камеры находится не одна частица, а много. Все частицы сосредоточены по периферии дробильной камеры в виде взвешенного постоянно перемешивающегося кольцевого слоя. Этот слой под воздействием молотков имеет свою окружную скорость vсл. При определении работы деформации при ударе по слою необходимо в расчет принимать относительную скорость движения молотков vот = vм - vсл .
Для разрушения материала необходимо, чтобы относительная скорость молотков была равна скорости, при которой произойдет разрушение зерна.
vот = vраз
Из опытов установлено, что скорость вращения слоя в молотковой дробилке
тогда
vот = vраз
где = 0,4...0,5 — коэффициент динамичности.
Тогда
т.е. скорость молотков должна быть в 1,6...2 раза выше разрушающей скорости. Поскольку в молотковой дробилке происходят многократные удары молотков по одному и тому же зерну, рабочую скорость молотков можно принимать несколько меньшей (на 15...20 %).
Скорость разрушения можно определить по теории Жуковского Н.Е., в соответствии с которой скорость разрушения при упругом ударе зависит от скорости распространения звуковых волн в разрушаемом материале:
где — разрушающее напряжение, равное временному сопротивлению при сжатии. Для зерен ячменя (наиболее прочное зерно) = 7МПа;
Е — модуль упругости зерна, Е = 840 Мпа;
С — скорость распространения звука в разрушаемом материале;
p – плотность материала, для ячменя p = 1300 кг/м3.
Тогда скорость разрушения материала
Если подставить значения физико-механических свойств зерна, то получится скорость разрушения vраз = 6,7 м/с, что в 8...15 раз меньше скоростей в дробилке. Это объясняется тем, что теория Герца действительна в пределах упругой области. У нас имеет место деформация за пределом упругости.
В соответствии с опытными данными Мельников С.В. предложил для определения разрушающей скорости зерна при многократном воздействии на него эмпирическую формулу:
где — характеристика физико-механических свойств зерна;
Кд — 1,6...2 — коэффициент динамичности;
— степень измельчения.
Дополнительная литература
1. Мельников С.В. Технологическое оборудование животноводческих ферм. - Л.: Агропромиздат, 1985.
Крупность частиц зерновых концентрированных кормов должна быть не более: для КРС — 3 мм, свиней и птицы — 1 мм, если эти концкорма используются для приготовления влажных мешанок. Если используют плющенное или экструдированное зерно, частицы допускаются более крупными. При этом пылевидных частиц должно быть минимально.
Любой корм до и после обработки не должен содержать в себе твердых примесей и металлических включений, семян сорных растений.
Влажность измельченных концентрированных кормов, подлежащих длительному хранению, не должна превышать 14...15 %.
Основы теории измельчения
Как указывалось, измельчение предусматривает разделение твердого тела на части. При этом образуются новые поверхности. Пусть имеется кубическая частица с размером ребра L. Ее общая поверхность составляет:

S = 6*L6
Если эту частицу измельчить таким образом, что получится n одинаковых кубиков, тогда длина ребра каждого из них составит
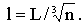
Площадь поверхности каждого кубика будет
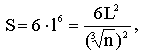
а всех n кубиков
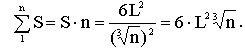
Сравнивая площадь кубика до дробления с суммарной площадью кубиков после дробления, можно написать
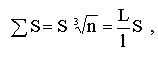
т.е. на сколько частей будет разделено ребро кубика, во столько же раз возрастет суммарная поверхность частиц.
Оценку развитости поверхности сыпучих материалов производят величиной удельной поверхности — отношением суммарной поверхности всех частиц к их массе или объему
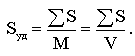
Например, для куба
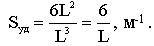
Крупность частиц того или иного кормового материала обуславливается зоотехническими требованиями. Для оценки затрат энергии, требуемой для перевода частиц от исходной крупности к заданной, необходимо знать степень измельчения, которая представляет собой отношение среднего размера частиц до измельчения (L или D) к среднему размеру частиц после измельчения (l или d)
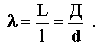
Степень измельчения можно выразить через удельную поверхность частиц. Учитывая, что L=6/Sуд и l=6/Sуд , можно написать
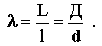
Процесс измельчения часто характеризуется также приращением удельной поверхности частиц:
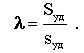
Обычно процесс измельчения изучается с двух позиций:
1. Выявляется зависимость между затратами энергии и степенью измельчения. Это позволяет выявить эффективность рабочего процесса, определить оптимальные рабочие органы применяемых типов машин и режимы их работы.
2. Определяется закономерность распределения измельченных частиц по крупности, что позволяет найти наиболее эффективные способы расчета средних размеров частиц, величин их удельной поверхности и численных значений степени измельчения.
Оба этих вопроса рассматриваются в энергетической теории измельчения.
Чтобы разрушить тело на части, необходимо приложить к нему усилие, большее, чем силы молекулярного сцепления. Силы молекулярного сцепления зависят от физико-механических свойств материала и поэтому могут быть различными. Работа внешних сил, затраченная на измельчение материала и отнесенная к единице массы или объема, называется удельной работой измельчения.
Еще в прошлом веке были предложены две энергетические теории измельчения: поверхностная и объемная. В соответствии с поверхностной теорией измельчения, которую предложил немецкий ученый П. Риттингер (1867 г.), работа измельчения прямо пропорциональна вновь образованной поверхности:
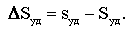
где a — коэффициент пропорциональности, учитывающий величину энергии молекулярного сцепления твердого тела.
Экспериментальные исследования показали, что поверхностная теория измельчения применима лишь при тонком измельчении. Для грубого измельчения русский ученый В.Л. Кирпичев (1874 г.) и немецкий ученый Ф. Кик (1885 г.) предложили объемную теорию измельчения, согласно которой работа измельчения прямо пропорциональна объему деформированной части тела
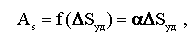
где k — коэффициент пропорциональности;
V — объем деформированной части тела.
Поскольку при измельчении могут получаться крупные и мелкие частицы, П.А. Ребиндер в 1928 г. предложил объединить обе теории в одну и рассматривать общую работу как сумму работ на образование новых поверхностей и деформацию, части объема тела
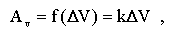
Анализируя приведенные зависимости, нетрудно убедиться, что для практического использования они малопригодны. С одной стороны, тяжело определить численные значения приращения поверхности и объема деформированной части тела, с другой — неизвестны коэффициенты a и k.
В 1952 г. С.В. Мельников предложил приближенную формулу для количественных расчетов работы измельчения в зависимости от степени измельчения:
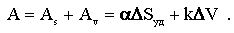
где С1 и С2 — коэффициенты, учитывающие удельные затраты энергии на измельчение и имеющие размерность удельной работы (Дж/ кг), определяются опытным путем. Например, для ячменя С1 = (10...13) 103 Дж/ кг, С2 = (6...9) 103 Дж/ кг.
Как мы уже говорили, при измельчении получаются частицы различного размера и тем более формы. Чтобы каким-то образом упорядочить размер и форму частиц для возможности дальнейших расчетов, принято приводить частицы неправильной формы к шару. При этом его диаметр определяется из фактического объема частицы неправильной формы. Определение объема частицы производят путем погружения отсчитанного их количества в мензурку с жидкостью, имеющий малый коэффициент поверхностного натяжения (керосин, ксилол, толуол и т.п.). Объем частицы определяется делением полученного общего объема на количество частиц в пробе
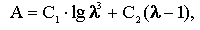
Тогда эквивалентный по объему диаметр частицы:
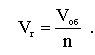
Было бы неправильным для определения эквивалентного диаметра брать частицы резко отличающихся размеров. А какие именно нужно брать?
В любом случае в массе измельченного материала размеры частиц подчиняются закону нормального распределения (закон Пуассона).
Этот график показывает, какой процент (или относительное количество) частиц имеет тот или иной размер. В любом случае частиц малого и большого размеров (диаметра) бывает меньше, чем среднего.
В зависимости от измельчающего рабочего органа кривая Пуассона может быть с высоким пиком или приплюснутая. Как оценить, каких частиц в массе материала больше? Для этого существуют различные методы определения среднего размера частиц: арифметический, геометрический, логарифмический, интегральный, взвешенный. Каждый из методов применим в определенных конкретных ситуациях.
Для практических условий наиболее пригоден метод определения средневзвешенного размера частиц. Это упрощенный среднеинтегральный метод. Если взять площадь под кривой и разделить на 100 % или Р, получим среднеинтегральный размер частиц. Но получить такую кривую сложно, да и обрабатывать ее трудоемко. Проще определить, сколько частиц данного размера находится в общей массе. Тогда получится гистограмма.
По сути она описывается кривой нормального распределения, но получить ее и обработать значительно проще.
Берут навеску разноразмерного материала и просеивают ее на ситах с разным размером ячеек. Размер частиц от 0 до d1 — проход через последнее сито, размер от d1 до d2 — остаток на последнем сите и т.д.
Размеры частиц остатка на первом сите обычно принимают равными:
где m — модуль сита — число, показывающее, насколько размер ячеек одного сита отличается от другого.
Как видно из гистограммы, средневзвешенный размер частиц можно определить по формуле:
Для зерновых кормов средневзвешенный размер частиц называется модулем помола.
В лабораторных анализах используют ситовой классификатор с набором из 10...12 сит с модулем m = 1,41 В производственных условиях используют классификатор из трех сит с размером ячеек 1, 2 и 3 мм. Тогда модуль помола:
где Р0, Р1, Р2, Р3 — процентное содержание фракций.
Для комбикормов принято считать М = 0,2...1 мм — мелкий помол, М = 1...1,8 — средний, М = 1,8...2,6 — крупный помол.
Рабочие органы, рабочий процесс молотковой дробилки
В мобильных заводах «BUSHOFF» применена дробилка закрытого типа с горизонтальным валом, решето и деки охватывают барабан до 300°. Материал удаляется по мере измельчения до заданного размера через отверстия решета.
Комбикормовые заводы «BUSHOFF» оборудованы циклонами с системой трубопроводов и фильтрами-пылеуловителями, образующими единую замкнутую пневмосистему. Это способствует обеспыливанию помещений.К рабочим органам относят молотки, решета и деки.
Для измельчения зерна используют пластинчатые молотки толщиной 6 мм.
Изготавливают молотки из марганцовистой стали 65Г с закалкой рабочих (активных) поверхностей или углеродистой стали с наплавкой кромок сармайтом.
Решета предназначены для отвода готового продукта, дополнительного его измельчения и регулирования степени измельчения. В мобильных заводах «BUSHOFF» применяют гладкие решета из листовой стали с пробивными круглыми отверстиями диаметром от 3 до 10 мм. Живое сечение решет составляет 0,08...0,35.
Процесс измельчения в молотковой дробилке происходит следующим образом. Зерна материала, попав в зону действия молотков, получают первый удар и отбрасываются к периферии, где отражаются поверхностью от деки или решета.
Отражаясь от них, частицы замедляют свое движение, но в зоне действия молотков они опять ускоряются от их ударов и потока воздуха. При установившемся процессе по всей внутренней окружности корпуса дробилки образуется вращающийся непрерывно перемешивающийся слой материала. От многократных столкновений с молотками, решетом и декой зерна измельчаются. При достижении заданного размера частицы материала проходят через отверстия решета и удаляются из дробилки. На их место поступают новые порции неизмельченного материала.
Работа деформации при ударе
Применительно к сельскохозяйственным материалам теорию о работе деформации при одиночном ударе в молотковой дробилке разработал В.П. Горячкин (см. собрание сочинений т.3. -М.: Колос, 1965).
Допустим, что между молотком и частицей происходит не упругий прямой центральный удар. Сопротивление молотку оказывает инерция частицы. В результате удара возникает импульс силы, который равен изменению количества движения:
i = M (vM - vk ), (1)
где М — масса молотка, кг;
vм и vк — скорость молотка до и после удара, м/с.
Если допустить, что начальная скорость частицы vr = 0, то изменение количества движения ее составит:
i = m * vk , (2)
где m — масса частицы, кг;
vк — скорость частицы после удара, равная скорости молотка после удара, м/с.
Импульсы сил, приложенных к частице и молотку, равны, поэтому равны и правые части уравнений (1) и (2)
M (vM - vk ) = m * vk
откуда
M * vM - M * vk = m * vk ,
M * vM = vk * (M + m) ,
или
(4)
Из формулы (4) видно, что конечная скорость зависит от соотношения масс соударяемых тел и изменяется по гиперболе. Если m <= M, то vм = vк.
Определим полезную работу молотка при его ударе по частице. Из курса теоретической механики известно, что при не упругом ударе часть кинетической энергии сохраняется для движения системы соударяющихся тел, а вторая часть превращается в работу деформации этих тел. Если сопоставить прочность молотка и измельчаемого материала, то можно заключить, что деформации и измельчению будет подвергаться менее прочный материал, каковым является корм. Поэтому всю работу деформации с известным допущением можно считать полезной. Найдем ее значение.
Полный запас кинетической энергии молотка при ударе
После удара кинетическая энергия молотка
Если допустить, что начальная скорость частицы ?r = 0, то и ее кинетическая энергия до удара равна нулю. После удара частица приобретает конечную скорость молотка и ее кинетическая энергия:
На основании закона сохранения энергии можно записать
A0 = Aм + Ar + Aдеф
откуда
Aдеф = A0 - (Aм + Ar )
или
Подставим из (3) значение mvk, тогда
(5)
Из уравнения (5) видно, что работа деформации прямо пропорционально зависит от скорости молотка или частицы после удара. При измельчении зерна обычно m < M и конечная скорость vм = vк . Тогда выражение (5) можно записать
(6)
Если m >> M, то конечная скорость ударяющего тела становится равной нулю. Такое явление наблюдается при ударе летящего зерна о деку. Таким образом, полученная от молотка кинетическая энергия зерна также расходуется на его деформацию при ударе о деку.
Тогда полезная работа от удара молотка по зерну составит
(7)
Уравнения для определения работы деформации получены с определенными допущениями.
Чем меньше масса измельчаемой частицы по отношению к массе молотка, тем с меньшим эффектом работает молотковая дробилка.
Необходимо отметить, что работа деформации, вычисленная по формуле (6), является максимально возможной для случая неупругого удара. На самом деле зерно и другие виды кормов обладают определенной упругостью, которая может быть учтена коэффициентом восстановления.
Тогда формулу (7) можно записать
(8)
По опытным данным для зерна средней сухости Купр = 0,3...0,4. Следовательно, при свободном ударе с учетом упругих свойств зерна лишь 84...91 % кинетической энергии от максимально возможной расходуется на разрушение. При измельчении зерна внутри дробильной камеры находится не одна частица, а много. Все частицы сосредоточены по периферии дробильной камеры в виде взвешенного постоянно перемешивающегося кольцевого слоя. Этот слой под воздействием молотков имеет свою окружную скорость vсл. При определении работы деформации при ударе по слою необходимо в расчет принимать относительную скорость движения молотков vот = vм - vсл .
Для разрушения материала необходимо, чтобы относительная скорость молотков была равна скорости, при которой произойдет разрушение зерна.
vот = vраз
Из опытов установлено, что скорость вращения слоя в молотковой дробилке
тогда
vот = vраз
где = 0,4...0,5 — коэффициент динамичности.
Тогда
т.е. скорость молотков должна быть в 1,6...2 раза выше разрушающей скорости. Поскольку в молотковой дробилке происходят многократные удары молотков по одному и тому же зерну, рабочую скорость молотков можно принимать несколько меньшей (на 15...20 %).
Скорость разрушения можно определить по теории Жуковского Н.Е., в соответствии с которой скорость разрушения при упругом ударе зависит от скорости распространения звуковых волн в разрушаемом материале:
где — разрушающее напряжение, равное временному сопротивлению при сжатии. Для зерен ячменя (наиболее прочное зерно) = 7МПа;
Е — модуль упругости зерна, Е = 840 Мпа;
С — скорость распространения звука в разрушаемом материале;
p – плотность материала, для ячменя p = 1300 кг/м3.
Тогда скорость разрушения материала
Если подставить значения физико-механических свойств зерна, то получится скорость разрушения vраз = 6,7 м/с, что в 8...15 раз меньше скоростей в дробилке. Это объясняется тем, что теория Герца действительна в пределах упругой области. У нас имеет место деформация за пределом упругости.
В соответствии с опытными данными Мельников С.В. предложил для определения разрушающей скорости зерна при многократном воздействии на него эмпирическую формулу:
где — характеристика физико-механических свойств зерна;
Кд — 1,6...2 — коэффициент динамичности;
— степень измельчения.
Дополнительная литература
1. Мельников С.В. Технологическое оборудование животноводческих ферм. - Л.: Агропромиздат, 1985.